Research

The Computational Dynamics Group (CODY) applies and develops theoretical and computational tools and methodologies in an interdisciplinary environment for understanding the behavior of nonlinear systems in different settings:

Topics

Biomathematics

Numerical and analytical study of mathematical models in Biomathematics.

Mathematical neuroscience. Mathematical neuron models, bifurcation analysis, design of new computational tools in neuroscience, fast-slow systems, bursting-spiking transition, coupled neuron systems (CPGs), neuron networks.
Non-linear cardiac dynamics. Mathematical myocyte models, bifurcation analysis, design of new computational tools in cardiac dynamics, cardiac arrhythmia.

Numerical detection of patterns in CPGs: Gait patterns in insect movement.
R. Barrio, Á. Lozano, M. Rodríguez and S. Serrano. Communications in Nonlinear Science and Numerical Simulation 82 (2020) 105047.
Bifurcations and slow-fast analysis in a cardiac cell model for investigation of early afterdepolarizations.
R. Barrio, M. Á. Martínez, L. Pérez and E Pueyo. Mathematics 8 6 (2020) 880.
Control strategies of 3-cell Central Pattern Generator via global stimuli.
Á. Lozano, M. Rodríguez and R. Barrio. Scientific reports 6 (2016) 23622.

Dynamical Systems

Development of new numerical methods for dynamical systems problems. Theoretical study of models.

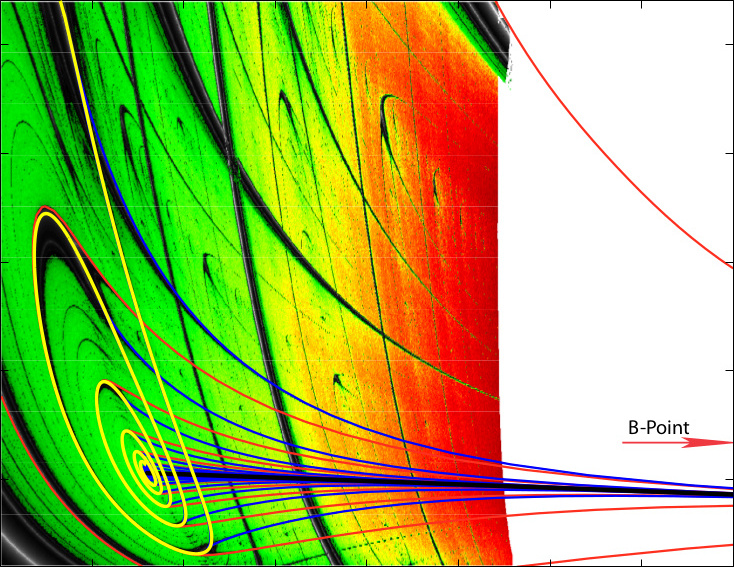
Dissipative systems. Low dimensional systems, crossroad formation in parameter space, homoclinic codimension-2 bifurcations, hyperchaos, periodically forced systems.
Computer Assisted Proofs. Rigorous proof of the existence of invariants.
Computational tools. Perturbation theory, bifurcation analysis, parameter sweeping techniques, Lyapunov exponents, chaos indicators.

Spike-adding structure in fold/hom bursters.
R. Barrio, S. Ibáñez, L. Pérez and S. Serrano. Communications in Nonlinear Science and Numerical Simulation 83 (2020) 105100.
Coexistence and dynamical connections between hyperchaos and chaos in the 4D Rössler system: A computer-assisted proof.
D. Wilczak, S. Serrano and R. Barrio. SIAM Journal on Applied Dynamical Systems 15 1 (2016) 356-390.
Topological changes in periodicity hubs of dissipative systems.
R. Barrio, F. Blesa and S. Serrano. Physical Review Letters 108 21 (2012) 214102.

Numerical Analysis

Design and theoretical study of new methods in Numerical Analysis, focusing in applications to Dynamical Systems

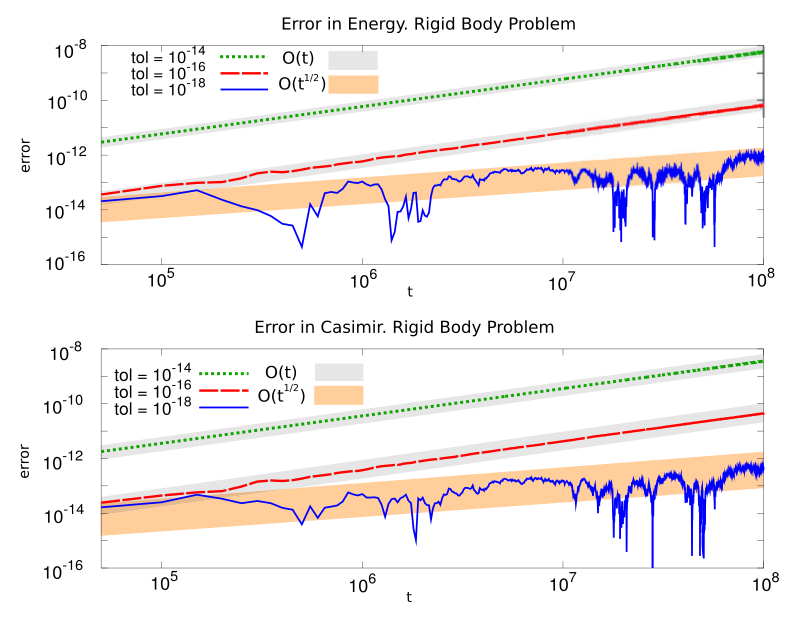
ODE and DAE systems. New numerical methods for ODEs, Taylor Series method.
Numerical linear algebra. Stability theory, evaluation of special functions, optimization algorithms, orthogonal polynomials and applications
High-precision numerical analysis. High-precision numerical linear algebra, high-precision solution of ODEs, rigorous computing.

ORTHOPOLY: A library for accurate evaluation of series of classical orthogonal polynomials and their derivatives.
R. Barrio, P Du, H Jiang and S. Serrano. Computer Physics Communications 231 2 (2018) 146–162.
A general condition number for polynomials
R. Barrio, H. Jiang and S. Serrano. SIAM Journal on Numerical Analysis 51 2 (2013) 1280-1294.
Algorithm 924: Tides, a Taylor series integrator for differential equations.
A. Alberto, R. Barrio, F. Blesa and M. Rodríguez. ACM Transactions on Mathematical Software 39 1 (2012) 5.

Full list of publications

Recent publications

A. Mayora-Cebollero, J. A. Jover-Galtier, F. Drubi, S. Ibañez, Á. Lozano Rojo, C. Mayora-Cebollero and R. Barrio. Almost synchronization phenomena in the two and three coupled Brusselator systems , Physica D: Nonlinear Phenomena 472 (2025) 134457. doi 10.1016/j.physd.2024.134457
S. Serrano, R. Barrio, Á. Lozano Rojo, A. Mayora-Cebollero and R. Vigara Benito. Coupling of neurons favors the bursting behavior and the predominance of the tripod gait, Chaos, Solitons & Fractals 184 (2024) 114928. doi 10.1016/j.chaos.2024.114928
Á. Lozano Rojo, R. Vigara Benito, R. Barrio and C. Mayora-Cebollero. Dominant patterns in small directed bipartite networks: ubiquitous generalized tripod gait , Nonlinear Dynamics 112 (2024) 15549–15565. doi 10.1007/s11071-024-09830-2
C. Mayora-Cebollero, A. Mayora-Cebollero, Á. Lozano Rojo and R. Barrio. Full Lyapunov Exponents spectrum with Deep Learning from single-variable time series , arXiv (2024).
H. Kitajima, T. Yazawa and R. Barrio. Fast-slow analysis and bifurcations in the generation of the early afterdepolarization phenomenon in a realistic mathematical human ventricular myocyte model , Chaos: An Interdisciplinary Journal of Nonlinear Science 34 12 (2024).
C. Mayora-Cebollero, A. Mayora-Cebollero, Á. Lozano and R. Barrio. Full Lyapunov exponents spectrum with Deep Learning from single-variable time series , Physica D: Nonlinear Phenomena (2024) 134510.
R. Barrio, S. Ibáñez and L. Pérez. Exploring the geometry of the bifurcation sets in parameter space , Scientific Reports 14 1 (2024) 10900.
S. Serrano, R. Barrio, Á. Martínez-Rubio, J. Belmonte-Beitia and V. M. Pérez-García. Understanding the role of B cells in CAR T-cell therapy in leukemia through a mathematical model, Chaos: An Interdisciplinary Journal of Nonlinear Science 34 8 (2024) 083142. doi 10.1063/5.0206341
R. Barrio, J. A Jover-Galtier, A. Mayora-Cebollero, C. Mayora-Cebollero and S. Serrano. Synaptic dependence of dynamic regimes when coupling neural populations , Physical Review E 109 1 (2024) 6337.
F. Drubi, A. Mayora-Cebollero, C. Mayora-Cebollero, S. Ibáñez, J. A. Jover-Galtier, Á. Lozano Rojo, L. Pérez and R. Barrio. Connecting chaotic regions in the Coupled Brusselator System, Chaos, Solitons & Fractals 169 (2023) 113240. doi 10.1016/j.chaos.2023.113240